Razonamiento Matemático: septiembre 2013

lunes, 30 de septiembre de 2013

Precio de compra y Precio de venta

Fórmulas :

Pv = Pc + G ó Pv = Pc - G

Ejm:

1.- ¿ A cómo se debe vender lo que costó S/30 para ganar el 12% del precio de costo?

Pv = Pc + G => Pv = 30 + 12%Pc
Pv = 30 + 12 Pc
100
Pv = 30 + 3.6
Pv = 33,6

2.- Un artículo cuyo precio de costo es S/84 se vende ganando el 20% del precio de venta. Hallar el precio de venta

Pv = Pc + G => Pv = 84+20%Pv
100% - 20% Pv = 84
80%Pv = 84
80 Pv = 84
100
Pv = 84 .100
80
Pv = S/ 105

EJERCICIOS

1.- Dos televisores fueron vendidos a S/3000 c/u. Si en el 1º se ganó el 25% y en el 2º se perdió el 25% ¿Hubo o no ganancia?
2.- Se vendió un equipo de sonido en S/640 ganando el 28% del precio de compra más el 10% del precio de venta. Halla el precio de compra
3.- ¿ A cómo se debe vender lo que me costó S/.5950 para ganar el 15% del precio de venta?

Porcentajes

Ejm:

1.- El 20% de que Nº es el 30% del 10% de 700

20 . x = 30 . 10 . 700
100 100 100

2x = 210
x = 105

2.- ¿ A cuánto equivale dos descuentos sucesivos de 40% y del 20% ?

Fórmula : Du = [D1 + D2 - (D1 x D2) ] %
100

Du = [ 40+20 - 40x20]%
100
Du = [60 - 8 ]%
Du = 52%

Aumetnos sucesivo:

Fórmula => Au = [ A1 + A2 + (A1xA2)]%
100

EJERCICIOS:

1.- Tres descuentos sucesivos del 25% 40% y 20%. Equivalen a un descuento único
2.- Luego de hacerle 2 descuentos sucesivos de 20% y 10%, un artículo cuesta S/ 288 ¿ Cuál es su precio original?
3.- Dos aumentos sucesivos del 20% y 30% y un descuento del 25%. Finalmente equivalen a un :

Regla de Tres

Regla de Tres Simple

a = > b DIRECTA (+) (+) x = c.b
c = > x a

a = > b INVERSA (+) (-) x = a.b
c = > x c

Ejm:

1.- Si por un cajón de 20 kg de naranja se paga S/24 ¿ Cuál es el precio por 7 kg?

DP (directamente proporcional)
+ +
kg S/. => X = 24.7 ( se simplifica)
20 24 20
7 x x = 6.7 /5
x = 42/5

2.- Si 21 obreros tardan 10 días en hacer una obra ¿ Cuántos obreros se necesitarán para hacer la misma obra en 15 días?

IP
+ -
Obreros Días = > X = 21 . 10 ( se simplifica)
21 10 15
x 15 x = 7.2
x = 14

Regla de Tres Compuesta

1.- Para pavimentar 180 m de pista, 18 obreros tardan 21 días. ¿ Cuántos días se necesitarán para pavimentar 120m de la misma pista con 4 obreros menos?

DP IP
m. obreros días = > x = 120 . 18.21 ( se simplifica)
- 180 + 18 + 21 180 . 14
+ 120 - 14 x x = 6 .3
x = 18 días

EJERCICIOS:

1.- Si 16 obreros trabajando 9 horas diarias en 12 días hacen 60 sillas ¿Cuántos días necesitarán 40 obreros trabajando 1 hora diaria menos para hacer un ciento de las mismas sillas?
2.- Un ganadero tiene 640 corderos que puede alimentar durante 65 días ¿ Cuántos corderos debe vender si quiere alimentar su rebaño por 15 días más dando la misma ración ?
3.- Una obra puede ser hecha por 20 obreros en 14 días ¿ Cuántos obreros hay que añadir para que la obra se termine en 8 días ?

Fracciones

Ejm:

1.- Halla los 2/3 de la mitad de los 4/5 de 3/10 de 500

4 . 3 . 500 = 120
5 10
=> 2/3 . 60 = 40
1 . 120 = 60
2

2.- El denominador de una fracción es 5 menos que el doble del numerador. Si el numerador aumenta en 8 y el denominador en 15, el valor de la fracción es 3/5. Hallar la fracción

f = a => a + 8 = 3
2a - 5 2a + 10 5
=> f = 10 = 2
5a + 40 = 6a + 30 15 3
10 = a

3.- La semana pasada se construyó los 4/7 de una pared y esta semana se han construido 5/12 del re4sto. Si aún falta 1m de altura por construir ¿ Qué altira deberá tener la pared?

pared : x construido falta construir

Sem. pasada 4/7 de x 3/7 de x
Esta sem. 5/12 de 3/7 de x 7/12 de 3/7 de x =1

=> 7 . 3 . x = 1
12 7
x = 4 m

EJERCICIOS:

1.- César pierde sucesivamente la mitad del dinero que tenía, la cuarta parte del resto y los 2/5 del nuevo resto. Si luego gana 1/3 del dinero que le quedaba ¿ Qué fracción del dinero original tiene ahora?
2.- Luis en su juego pierde 1/3 de su dinero, en el 2º pierde 1/4 del resto y en el 31 pierde 1/5 del nuevo resto. Si al final se quedó con S/120. Halla el dinero con el que empezó a jugar
3.- Jorge regala 2/5 de su dinero a Fátima y aún le quedan S/900 ¿ Cuánto tenía?

Razones y Proporciones

Ejm:

1.- Dos números están en relación de 4 a 5 y su suma es 72. Hallar el mayor de dichos números.

A = 4 = 4k
B 5 5k => 4k + 5k =72 = > Mayor número : 5k = 5(8) = 40
9k =72
k = 8

2.- Dos números son entre si como 5 es a 8. Si la suma de sus cuadrados es 712. Hallar dichos números

A = 5 = 5k => (5k)² + (8k)² = 712 => A = 5k
B 8 8k 25k² + 64k² = 712 = 5(2√2)
89k² =712 A = 10√2
k² = 8
k = √8 B = 8k
k = 2√2 = 8(2√2)
B = 16√2

3.- Dos números son entre si como 7 es a 13. Si al menor se le suma 140 para que el valor de la razón no se altere, el valor del otro número debe quintuplicarse. Hallar el mayor

a = 7k => 7k + 140 = 7 => 7k + 140 = 35k
b 13k 5(13k) 13 140 = 28k
5 = k

=> Mayor nº "b" : 13k = 13(5) = 65

EJERCICIOS

1.- En un salón de jardín la relación entre el Nº de niños y niñas es de 4 a 3. Si después de 2 horas, 8 niños son recogidos por su mamá y a la vez llegan 5 niñas entonces la nueva relación será de 2 a 7. Halla el Nº de niños que quedan
2.- Dos números son entre sí como 8 es a 15. Si al menor se le suma 112, para que el valor de la razón no se altere, el valor del otro número debe trilpicarse ¿ Cuál es el valor de a +b ?
3.- En una reunión estudiantil la relación de muejres y hombres es de 3 a 4. En un momento dado se retiran 6 damas y llegan 3 hombres con lo que la relación es ahora de 3 a 5 ¿ Cuántas muejres deben llegar para que la relación sea de 1 a 1 ?

Edades

Ejm:

1.- Si al triple de la edad que tengo se quita mi edad aumentada en 8 años, tendría 36 años ¿ Qué edad tengo?

Edad : x => 3x - ( x + 8 ) = 36

3x - x - 8 = 36

2x = 44

x = 22

2.- Elsa es 6 años más joven que Ivan. Hace 3 años Ivan tenía el triple de la edad que Elsa tenía entonces . Encontrar la edad de Ivan

pasado presente = > x - 3 = 3(x - 9)

Elsa x - 9 x-6 x - 3 = 3x - 27

Ivan x - 3 x 24 = 2x

12 = x

3.- Miguel le dice a Ana: Yo tengo 20 años; mi edad es la mitad de la que tendrás cuando yo tenga la edad que tú tiened ¿ Qué edad tiene Ana?

Presente Futuro

Ana x 2(20)

Miguel 20 x => 2x = 60

x = 30

EJERCICIOS:

1.- 3 veces el producto de la edad de nataly disminuuido en uno, con su edad aumentada en 3 es 63. Hallar dicha edad

2.- La edad de Denise es el cuádruplo de la edad de Coronado. Hace 5 años la suma de sus edades era 40 años ¿ Qué edad tiene Coronado?

3.- Un padre le dice a su hijo: hace 8 años mi edad era el cuádruplo de la edad que tú tenías, pero dentro de 8 años únicamente será el doble ¿ Cuál es la edad del hijo?

Ecuaciones

Ejm:

1.- En una reunión se cuentan tantos caballeros como 3 veces el número de damas. Después llegan 300 caballeros más y 40 damas más y ahora para cada dama hay 5 caballeros. ¿ Cuántas damas había al comienzo?

INICIO DESPUÉS

Caballeros = 3x Caballeros = 3x + 300
Damas = x Damas = x + 40

Resolución

damas = 1 x + 40 = 1
caballeros 5 => 3x + 300 5 => 5x + 200 = 3x + 300
2x = 100
x = 50

2.- Una persona tiene S/ 20.000 y otra S/ 7500, cada una ahorra anualmente S/ 500 ¿ Dentro de cuántos años la fortuna de la primera será el doble de la segunda?

1º persona : 20000 => 20000 + 500x
2º persona: 7500 => 7500 + 500x

Resolución : 20000 + 500x = 2(7500 + 500x)
20000+ 500x = 15000 + 100x
5000 = 500x
10 = x

3.- Hallar dos números cuya suma sea 60 y el cociente de sus recíprocos es 3. Dar como respuesta el quintuplo del mayor aumentado en 8.

x + y = 60 y = 3
x
x = 60 - y
y = 3 => y = 180 - 3y => 5y + 8
60 - y 1 4y = 180 5(45) +8
y = 45 233

4.- El doble de mi edad, aumentado en su mitad, en sus 2/5, en sus 3/10 y en 40; suma 200 años. ¿ Cuántos años tengo?

Mi edad : x => 2x + x +2x+3x+40 = 200
1 2 5 10
20x + 5x + 4x + 3x + 400 = 200
10
32x + 400 = 2000
32x = 1600
x = 50

5.- Se compra cierto número de relojes por S/ 5625, sabiendo que el número de relojes comprados es igual al precio de un reloj en nuevos soles. ¿ Cuántos relojes se han comprado?

Nº de relojes: x => x . x = 5625
Precio de c/ reloj : x x² = 5625
x = √5625
x = 75

EJERCICIOS

1.- Cierto número de personas alquilan un camión en 320 dólares; en el momento de la salida, faltan 2 personas; y por eso los demás tienen que pagar cada uno 8 dólares más ¿ Cuántas personas había al contratar el camión?
2.- Si al numerador de la fracción 3/5 se le suma un número y al denominador se le resta el mismo número se obtiene otra fracción equivalente al recíproco de la fracción dada. Calcular el número
3.- Dos recipientes contienen 80 y 150 litros de agua y se les añade de la misma cantidad de agua a cada una ¿ Cuál debe ser esta cantidad para que el contenido del primer recipiente sea los 2/3 del segundo?

Series

Serie aritmética

Para hallar el término "n" :
an = a1 + (n - 1) r

Para hallar la suma:
S = (a1 + an) n
2

Ejm:

Hallar el valor de :

S = 3 + 10 + 17 + ...+ 164 + 171 -- 25 términos

+7 +7

S = (3 + 171) 25

S = 1275

--> Hallar el término "n"

an = a1 + (n -1) r

an - a1 = (n - 1) r

an - a1 = n - 1

an - a1 +1 = n
r
(171 - 3) + 1 = n
7
25 = n

Serie geométrica:

Fórmula general:

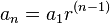~~$a_n = {a_1}{q^{(n-1)}}\,$~~

Para hallar la suma:

S = a1 . ( q^n-1)

q - 1

Ejm:

Hallar el valor de "n"

S = 3 + 6 + 12 + 24 + ... + 1536

x2 x2

an = a1 . q^n-1

^{1536 = 3.2}^n-1

^{512 =2}^n-1

^{10 = n}

Series Notables

* 1 + 2 + 3 + ... + n = n(n+1)

* 2 + 4 + 6 + ...+ 2n = n(n+1)

* 1 + 3 + 5 +...+ 2n - 1 = n²

* 1² + 2² + ..+ n² = n(n+1)(2n+1)

* 1³ + 2³ + 3³ + ..+ n³ = [n(n+1)]²

* 1x2 + 2x3 + 3x4 + ... + n(n+1) = n(n+1)(n+2)

* 1x2x3 + 2x3x4 + .... + n(n+1)(n+2) = n(n+1)(n+2)(n+3)

sábado, 28 de septiembre de 2013

Sucesiones

Sucesión polinomial de primer orden, lineal o aritmética:

Toda sucesion lineal tiene la forma

an = an + b

Ejm:

Hallar el término enésimo en la siguiente sucesión

1° 2° 3° 4° 5°

5 ; 9 ; 13 ; 17 ; 21 ; ...

+4 +4 +4 +4

a1 = 4(1) + 1

a2 = 4(2) + 1

a3 = 4(3) + 1

an = 4(n) + 1

EJERCICIOS

1.-Hallar el término enésimo en : 3; 10; 17; 24; 31; N

2.-Hallar el término enésimo en: 56; 50; 44; 38; N

3.-Hallar el término enésimo en: 7; 11; 15; 19; N

Sucesión polinomial de segundo orden o cuadrática:

En toda sucesión cuadrática el término enésimo tiene la forma:

an = an² + bn + c

Ejm:

Hallar el término enésimo en la siguiente sucesión:

a0 = 1 ═► 5 ; 11 ; 19 ; 29 ; 41 ; ....

m0 = + 4 ═► +6 +8 +10 +12

r = +2 ═► +2 +2 +2

a0 = r/2 b = m0 - a c = a0

a = 2/2 b = 4-1 c = 1

a = 1 b = 3

an = n² + 3n + 1

EJERCICIOS:

1.- Hallar el término enésimo en : 6; 13; 24; 39; 58

2.- Hallar el térmiino enésimo en: 2; 7; 13; 20; 28

3.- Hallar el término enésimo en: 3; 13: 27; 45; 67

Sucesión geométrica:

Tiene la siguiente fórmula general:

an = a1 . rᶰ-¹

Ejm:

Hallar el término enésimo:

2 ; 6 ; 18 ; 54 ; 162

x3 x3 x3 x3

a1 = 2 x 3°

a2 = 2 x 3¹

a3 = 2 x 3²

a4 = 2 x 3³

an = 2 x3 ᴺ-¹

EJERCICIOS:

1.- Hallar el término enésimo en : 3; 15; 45; 225; N

2.- Hallar el término enésimo en: 4; 8; 16; 32; 64; N

3.- Hallar el término enésimo en : 1; 7; 49; 343; N

Vistas de página en total

lunes, 30 de septiembre de 2013

sábado, 28 de septiembre de 2013