Series

Serie aritmética

Para hallar el término "n" :
                     an = a1 + (n - 1) r

Para hallar la suma:
                              S = (a1 + an) n
                                           2

Ejm:

Hallar el valor de : 

    S = 3 + 10 + 17 + ...+ 164 + 171   --  25 términos

                  +7        +7

       S = (3 + 171) 25  

                    2

          S = 1275  

--> Hallar el término "n"    

       

        an = a1 + (n -1) r          

         an - a1 = (n - 1) r

         an - a1 = n - 1

             r              

        an - a1 +1 = n
            r
         (171 - 3) + 1 = n
               7      
             25 = n


Serie geométrica:

Fórmula general: 

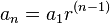Para hallar la suma:

       

                               S = a1 . ( q^n-1) 

                      q - 1

Ejm:

Hallar el valor de "n"

              S = 3 + 6 + 12 + 24 + ... + 1536

                  x2   x2

    an = a1 . q^n-1

      

    ^{1536 = 3.2n-1}

      ^{512 =2n-1}

       ^{10 = n}    

Series Notables

* 1 + 2 + 3 + ... + n = n(n+1)

                                         2

*  2 + 4 + 6 + ...+ 2n = n(n+1)

*  1 + 3 + 5 +...+ 2n - 1 = n²

*  1² + 2² + ..+ n²  = n(n+1)(2n+1)

                                      6

*  1³ + 2³ + 3³ + ..+ n³ =  [n(n+1)]²

                                             2

*  1x2 + 2x3 + 3x4 + ... + n(n+1) = n(n+1)(n+2)

                                                             3

*  1x2x3 + 2x3x4 + .... + n(n+1)(n+2) = n(n+1)(n+2)(n+3)

                                                                        4